Imaginary Numbers

Explanation of the Math

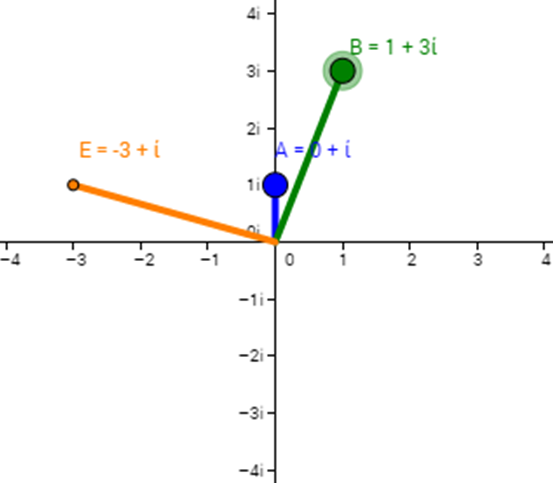
As noted earlier complex numbers have the form a+bi where a and b are real numbers. An easy way to see a representation of them is to graph them on the complex plane since they don't fit on the number line. The x-axis is still the x-axis but the y-axis will become the imaginary axis. So the complex number 1+3i would be 1 unit right and then 3 units up. If you multiply any complex number (a+bi) by i you get i*(a+bi) = ai + bi² = -b + ai which will rotate you point 90° CCW. (Mazur, 2003)

Addition, Subtraction, Multiplication, Division

Add the imaginary components together and add the real components together. So (2+2i) + (1+4i) = 3+6i. Subtraction is similar. Subtract the imaginary components and subtract the real components. (2+2i) - (1+4i) = 1 - 2i. Multiplication is a little bit more complicated but it goes as follows. (a+bi)*(c+di) = ac + bci + adi + bdi² since i² = -1 then this can be rewritten as ac-bd + (bc+ad)*i. Then division is more complicated. This applet will allow you to visually explore addition, subtraction, multiplication and division.

Where do these i's even come from though? How do I go from a number with an imaginary part to the equivalent number with a square root? Here is the relationship. a+bi = a+b√(-1) = a+ √(b*b*-1) = a+ √(-b*b). To give an example we have 5+3i = 5+3√(-1) = 5+√(3*3*-1) = 5+√(-9). For a more in depth look, you can visit the Khan Academy website. There is a unit about the introduction of the imaginary unit i. There is another unit about Imaginary and complex numbers. Then even a third about Factoring using imaginary numbers. (Khan, 2014). With Khan Academy, there are videos that teach you the concepts and then there are exercises that provide opportunities for you to prove that you understand the concepts and have developed the skills to work out the exercises.

Conjugate Pairs

An important thing to remember about imaginary numbers is that they come in pairs. These pairs are called conjugates. The conjugate is the complex number that has the same real component but a negative imaginary part. For example: 1-i is conjugate pair of 1+i because the imaginary components are the negative value of each other. Every conjugate has the characteristic that when we multiply them together we get a number that does not have an imaginary component. For example: 1+i-i-i² = 1-(-1) = 2. It would be a good idea now to use an applet to visually see how conjugates work with addition, subtraction, multiplication and division.
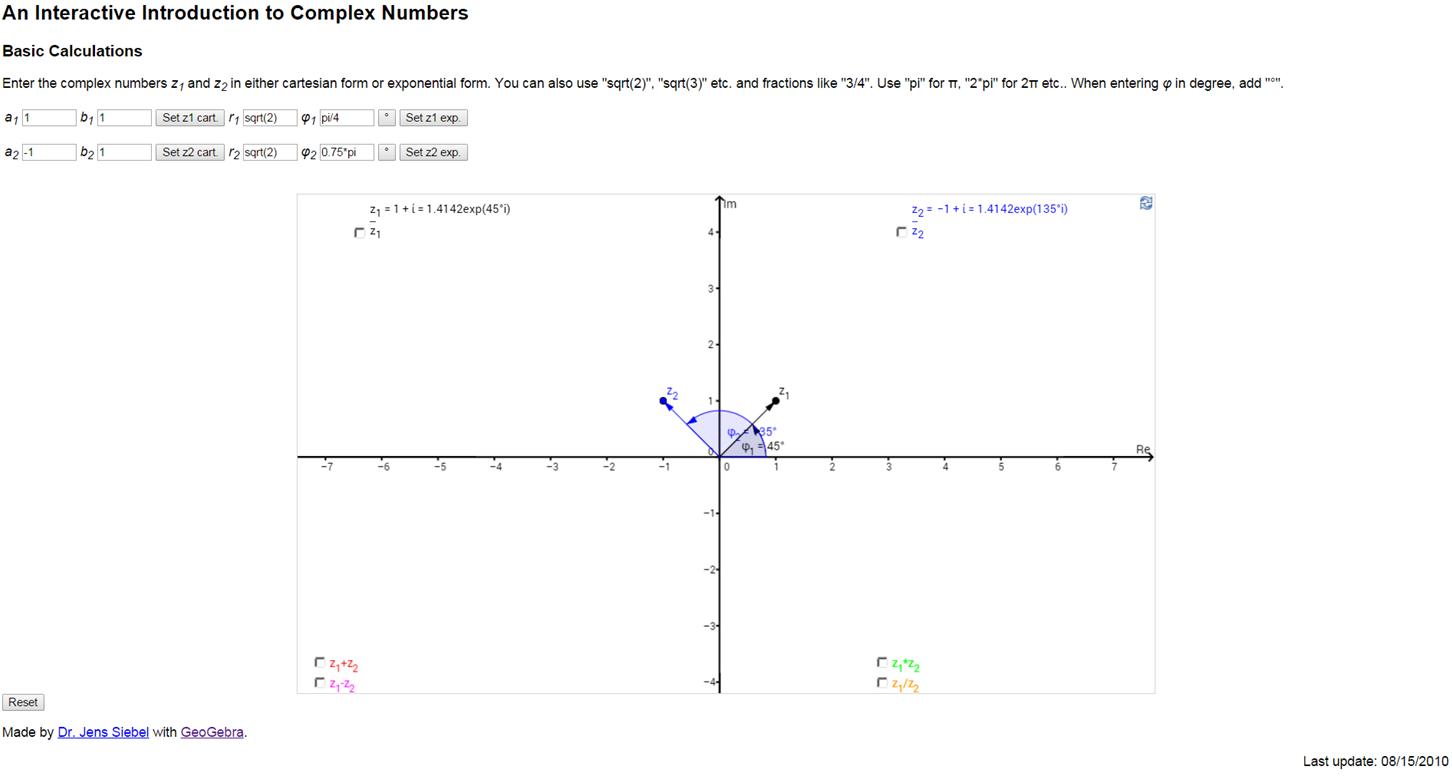
There is a great applet created by Dr. Jens Siebel that will do all of those operations. (Siebel, 2014) Using z1 and z2 you can program the two complex points on the graph. The check boxes below the points toggle the complex conjugates pairs on and off. Once the points are plotted then there are check boxes to trigger all of the mathematical operations. You can add, subtract, multiply and divide any two complex numbers. The points may not always be visible (because they are off the graph) but the result of the operation is always shown by the check box itself. This applet created by Dr. Jens Siebel.