 11
11
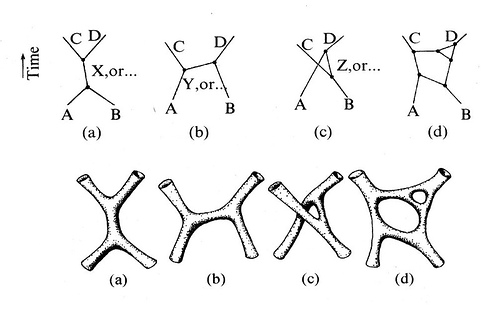
This picture illustrates the "strings" of string theory. If you're a physics major, think Feynman diagrams.
back to main page
Transformations in general everyday geometry used to find areas and distances (e.g., rotating a triangle in a coordinate system so that the base lies along the x-axis or
changing from cartesian -x,y,z- coordinates to sphyrical -distance from origin, latitude angle, longitude angle- coordinates) have many clear applications in simplifying
real-life problems -although, of course, they have been studied apart from application as well.
But what about more complex topology?
Mathematics related to curved surfaces was initially developed by mathematicians as purely math, but was later used by physicists (starting with Einstein) in the theory of general relativity; higher-dimensional topology was also originally developed by mathematicians as purely math -of course you'd expect there to be no use for it... we live in a 3-dimensional world, so who cares about mathematics with 8-dimensional or 14-dimensional equations?- but now string theory, a model many physicists hope will succesfully explain things that physics currently doesn't understand, uses 10- and 11- dimensional mathematics that is "super-symmetric", and has not only taken advantage of the higher-dimensional mathematics that had already been developed by mathematicians, but motivated the exploration of "super" stuff in these higher dimensions which has yielded new mathematical knowledge.2
What all that "super" stuff means is complicated (and physicists are actually doubting some of the supersymmetry stuff that is in certain versions of string theory now anyway),
but the point I want to bring out here is how physics and mathematics have worked together in developing new knowledge.
 11
11
This picture illustrates the "strings" of string theory. If you're a physics major, think Feynman diagrams.
back to main page