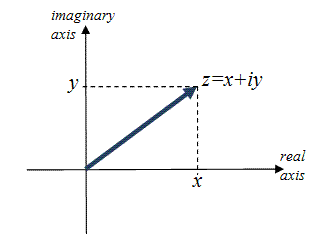Let's Get Real Here
The imaginary numbers were first discovered by Girolamo Cardano who
lived during the Renaissance (1501-1576). He was a physician, philosopher,
mathematician, astrologer, and prolific writer. As he spent most of his
youth gambling, he was able to develop many cognitive and problem
solving strategies. He obtained a Doctorate in medicine from Padua,
however his study of medicine came to an end when he wasn't accepted
into the College of of Physicians. He then devote his time to his
greatest work, the Ars Magna (The Great Art). There was only one
instance where he included his discovery of imaginary numbers. By
solving the equation x(10-x)=40, he obtained the roots 5+√-15
and 5-√-15. However, he noted these roots as
useless.
Within his work, he also included his discoveries from working with the cubic equation x3+px=q. When
attempting to solve it, he comes across imaginary numbers once again and dismisses them.So, in order to avoid imaginary numbers, many mathematicians wrote
their equations with only positive terms. Rafael Bombelli was the first mathematician that took particular attention to the imaginary numbers. He worked a lot
with the Ars Magna. He was intrigued by the idea of taking the square root of a negative number. Although his discoveries didn't lead to a full understanding and acceptance of imaginary numbers, it
brought them out of the dark, scary abyss and into the light.
Girolamo Cardano Rafael Bombelli


Next to come along was Rene Descartes (1596-1650). In his last book of the Geometrie, he he worked mainly with algebra. By taking all terms of an
equation to one side and setting it equal to zero, he discovered many properties concerning the polynomial's roots. If a is a root of f(x), then the
corresponding linear polynomial (x-a) is a factor of f(x). In his work, he also provides a proof of his theorem that states, "Any equation of degree n
has n roots." Descartes also became very well known for his rule of signs. Given an equation:
f(x)=aoxn+a1xn-1+...+an-1x+an=0, ao>0,
the number of positive real roots is less than or equal to the number of sign changes. Similarly, the number of negative real roots is less than or equal to
the number of sign changes in f(-x). However, since the sum of the number of positive and negative real roots isn't always equal to n, this this gave rise
to the existence of imaginary roots.
Now have the ability to graph complex numbers. The y-axis becomes the imaginary axis, and the x-axis is the real axis. This is called the complex
plane.
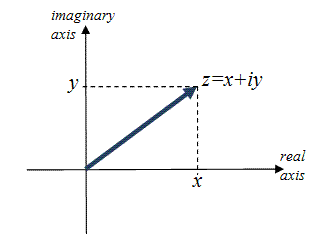
Mathematicians in today's world are familiar with i as the representation for √-1. This notation was introduced by Leonhard Euler in
the 1700s. Another neat property of imaginary numbers is that:
i0=1
i1=i
i2=-1
i3=-i
i4=1
i5=i
i6=-1
i7=-i
And this pattern continues to repeat. So, in=in(mod 4).