
As is seen in the history of the development of set theory, it has been a dynamic field of study which deeply impacts the way in which mathematicians think about and approach their subject. In 1965, Dr. L.A. Zadeh(pictured right) of University of California Berkeley published his first paper(and only one of its kind) on what he dubbed to be "fuzzy sets." His theory was not immediately accepted, and many of his colleagues were shocked that Dr. Zadeh, who up until this point had dealt with unambiguous material relating to control theory would venture out into the world of uncertainty which previous mathematicians tried to avoid.
Typically the study of logic deals with the study of statements that are either true or false. But, what if we are dealing with a statement that does not have a clear-cut true or false value? For example what if the question of who is funny is posed. Or, who is middle-aged? It is subject to subjectivity, correct? However, there are similar propositions to this that are not nearly as trivial that impact the world in which we live. This uncertainty, or ambiguity is different from the uncertainty that we experience in probability. According to Dr. Masao Mukaidono, probability deals with uncertainty with respect to randomness, and the uncertainty stems from the fact that the future cannot be known, only predicted. On the other hand, fuzzy logic deals with uncertainty stemming from subjectiveness, even when the event has passed, there is still uncertainty. Sets arising from such statements or questions do not have the "crisp" binary quality of typical set theory(axiomatic). Thus, earlier arguments that fuzzy theory is merely mirroring the study of probability does not hold up due to the different types of uncertainty that exist.
Instead of the binary system associated with set theory, elements are assigned a possible degree to which they are either in or out of the set. This is expressed as any number between or including 1 and 0. For instance, in the example of the set of all middle-aged individuals, the age of 34 may be assigned .2 while the age of 49 may recieve a 1. Unlike probability, the degrees to which each element is included in the set does not have to add up to 1.
What does this mean for determining the intersection of two fuzzy sets? This means that, is in the nature of a single set, there exists "degrees of intersection." It can also be looked at, in some cases, and the degree of possibility that two fuzzy sets intersect. There is a vast amount of information on this topic, and for the sake of time, I will refer you to my resources page for more information. There is just so much to cover!
The first application of Fuzzy Theory was the emergence of "fuzzy control" in engineering. It was first used in automatic controls of a steam engine in London, England in 1974. Next, it was applied in Japan in water purifier systems. How is this so? How does it differ from applying axiomatic set theory and binary logic? Computers run in the world of a binary system, which is run on symbolic logic. However, the way we as humans think is semantic.
"The essential uncertainty of human beings might come from the language we have used to communicate in because the semantics are uncertain. Information that we want to express is continuous and analog. But, we can communicate with each other with the digital symbols of language. The semantics of the transferred symbol are reconstructed in each mind. For human and computer interaction computers need to understand the semantics of our language. Computers receive a language, and then look up the semantics of the words. The syntax and the semantics correspond to a fuzzy set and a membership function.
"Fuzzy Theory provides a method for computers to quantify the semantics of the language. The uncertainty of the language caused by subjectivity is represented by a membership function which gives arbitrary precision to expressions. The computer can have a knowledge only if it stores the quantified semantics of language in its internal memory. The fuzzy theory aims to provide an effective tool for humans and computers."
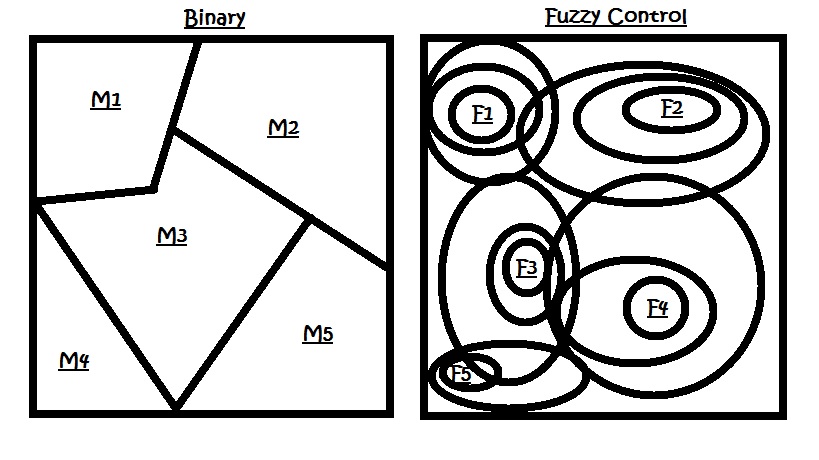
Japan is the current leader in the world for fuzzy applications. Fuzzy control, most commonly used, aims to take semantic language and quatnify it by having professionals define it through a number of membership functions. Unlike fuzzy inference(see Resources) which results in another fuzzy set, fuzzy control results in a single value from which computers can act on within the binary system. This system allows movements to change slightly as opposed to abruptly. The fuzzy system takes every element into account(not to mention the degree to which each element is part of a certain set). Keep in mind that these fuzzy "rules" are developed by professional people, and those dictate the nature of the system. This can be seen in the following visual of a binary system and a fuzzy system:

As you can see, the purely binary system is very rigid, if the system were to receive information of a certain condition, it would automatically adjust rapidly. In contrast, there are far more variables in play that cause a change in a system to be gradual.
Many mathematicians suggest that fuzzy theory be applied to the social science, where subjectiveness and uncertainty are commonplace. Unfortunately, many of the social science community is not familiar enough with fuzzy theory to use it effectively, or at all. Mukaidono believes that in the future it will be used more readily in social science fields of study.
In the meantime, fuzzy theory is being used to run an "un-manned" train and control subway systems, control systems for automatic elevators, temperature control in blast furnaces for glasses, cooling and incinerating process control, controller for a welding robot and an automatic car speed controller, to name a few.
A. Recall our study of the nature of fuzzy sets. Why would the graph of Set A in Fuzzy Theory look like this, compared to the axiomatic set A which an element is either in or out?
B. With a partner, discuss the significance of a binary system in axiomatic set theory, and the significance of a nonbinary system in fuzzy logic.
C. From our discussion, how would you compare and contrast the union of set A and B in Axiomatic Set Theory and Fuzzy Set Theory?
D. Make a conjecture as to why the complement of set A in the world of Fuzzy Set Theory constructed this way.
1. Now that you have explored two types of set theory simultaneously, hypothesize(or give examples) what type of propositions would create sets that are binary(every element is clearly in or out of the set), or sets that fall under the umbrella of axiomatic set theory?
2. What kind of propositions would yield sets that fall into the category of fuzzy set theory?