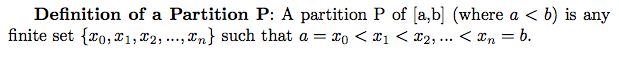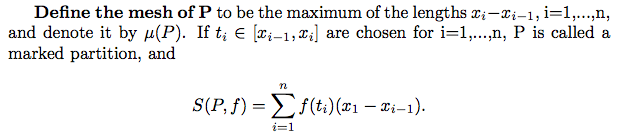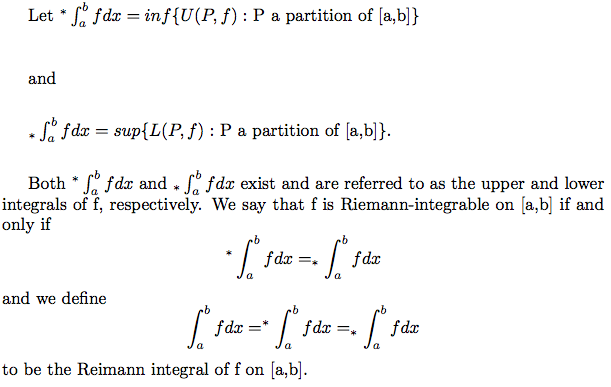Explanation of Mathematics

First of all, lets review the limit definition of a derivative and where it comes from:

Derivative




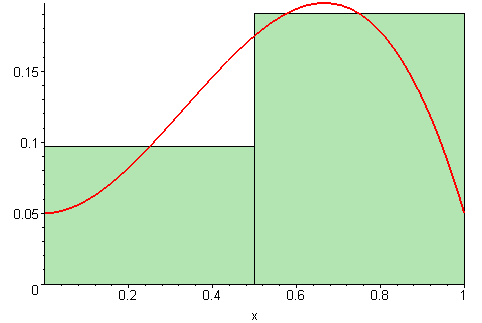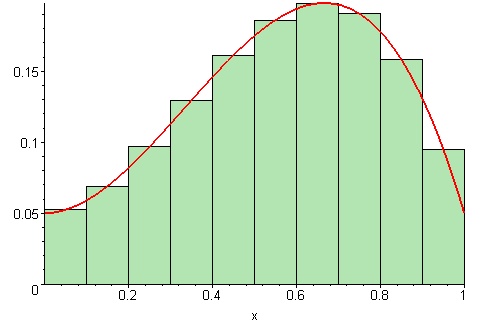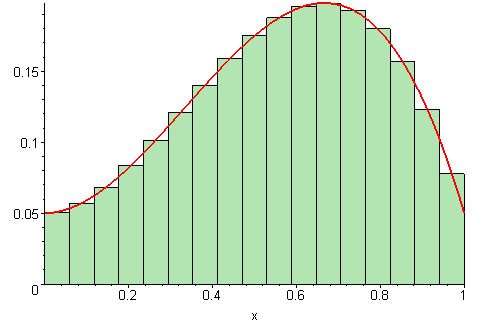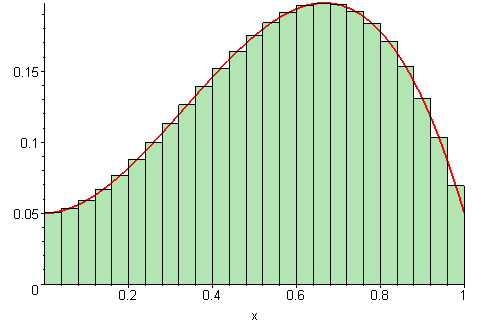
Now, we know from the history of how integration was explored and discovered came not from antiderivatives, but from simply trying to find the area under the curve. The link between derivation and integration did not come until much later. So let's explore area under the curve. One method that many mathematicians used is what we call the Riemann Sum today. This method splits the area under the curve into smaller and smaller inscribed rectangles:
Riemann Sum


But still, this alone doesn't explain why integration and derivation are inverse operations. Why in heavens name does taking an antiderivative give us the area under the curve?

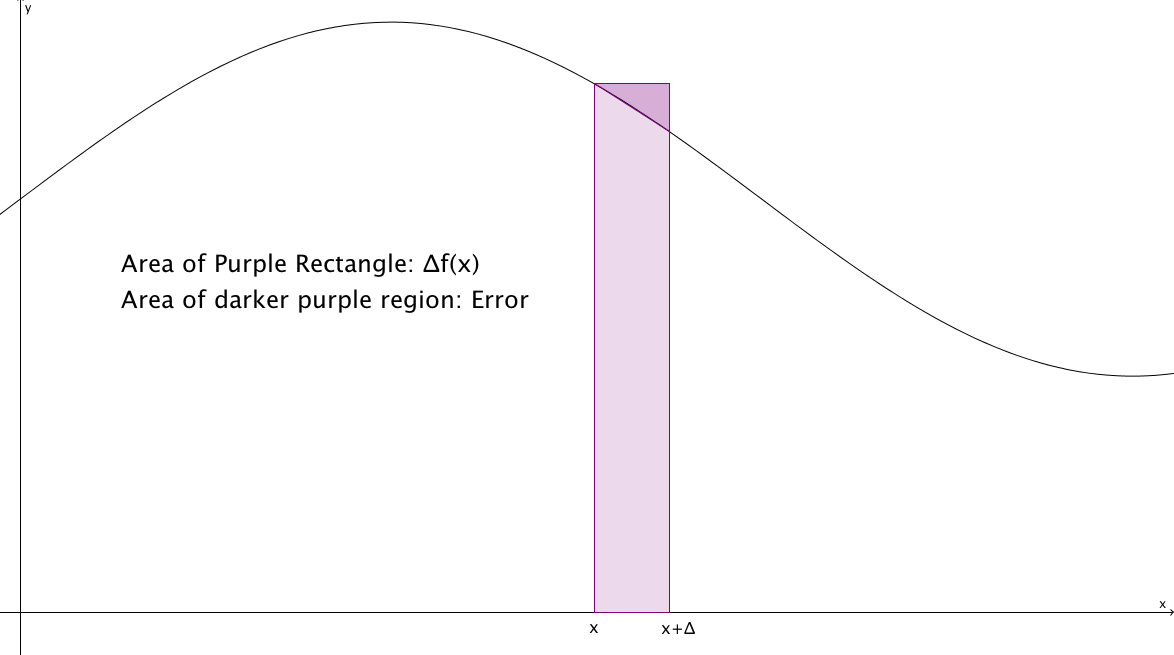
With the definition of a derivative under our belts, it looks like we are ready for an

Informal Proof of the Fundamental Theorem of Calculus.



Use this applet as you read the proof to discover the integral on your own! informal Proof informal Proof informal Proof


Practice with taking derivatives makes finding some antiderivatives easy- but as you have probably seen before, finding a closed form antiderivative can often be very complex and is sometimes even impossible. In cases where finding an antiderivative is impossible, we can use other methods such as the Riemann Sum (which uses this same idea of inscribing rectangles of smaller and smaller width) to numerically approximate the area under a curve. Why would we go to all of this trouble? Why is finding area under a curve significant? Find out here .

An informal proof is helpful to clarify theorems and to give us a better idea of why things work the way they do. But they should never be a replacement for a formal proof that proves our theorem generally for all cases, without any holes or fallacies. Before we begin a formal proof of the Fundamental Theorem of Calculus, there are some definitions and background information that we need to be aware of:

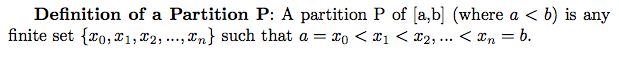
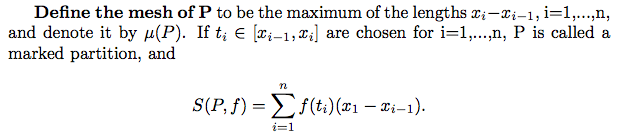
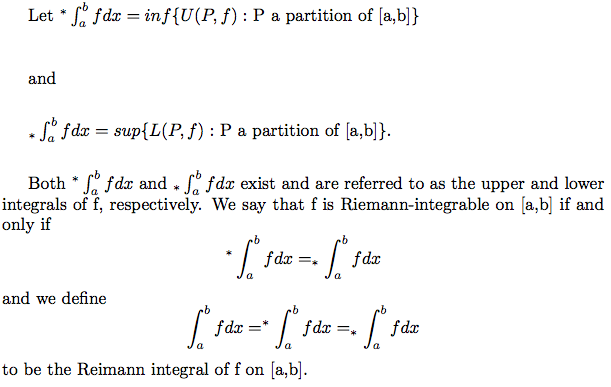
partition mesh Riemann Integral Riemann Integral


Now we have all of the info we need to give a formal proof of the

Fundamental Theorem of Calculus

(How exciting!!)

Formal Proof Formal Proof


(Gaughan, 2009 pp. 137-154)