Mathematics

Mathematics of the Golden Ratio

Euclid described the golden ratio as the "dividing a line in extreme and mean ratio" He used the following illustration to show what this meant:

What Euclid meant by the "dividing line in extreme and the mean ratio" was that the mean ratio was when the ratio of segment AB to AC was equal to the ratio of segments of AC to BC or when AB/AC = AC/BC. He found that this only occurs at the golden ratio. Use the following Geogebra applet to test this for yourself Golden Section Applet .
The Fibonacci sequence is the series of \(A_{n+2} = A_{n+1}+A_{n}\) such that \(A_{n} = 0\) and \(A_{n+1}=1\) this gives us the sequence \(0, 1, 1, 2, 3, 5, 8, 13, . . . \) (Dunlap 1997) If we take the ratio of successive terms of the Fibonnaci sequence it appear as if the ratio will converge to the golden mean. Try this out for yourself. Divide successive terms of the Fibonacci sequence and see if you get anything near to the golden ratio. Click the show table button below to check your answers.

A proof of this convergence can be seen as follows
\[f_{n+1}/f_{n} = (f_{n}f_{n-1})/f_{n} = 1 + (f_{n-1}/f_{n})\]
Now we substitute \(x\) for \(f_{n+1}/f_{n}\) and we obtain the following: \[x = 1 + 1/x\] \[x^{2} - x - 1 =0\] \[x=\dfrac{1+\sqrt{5}}{2}\approx 1.61803\] (Dunlap 1997) and (Popa-Dăbuleanu)

The Pythagoreans worked with several different geometries that contain the golden ratio. Some of their more famous work involving these ratio were the golden rectangle and pentagram

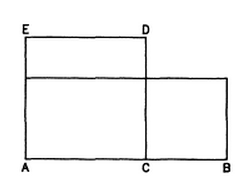
Let's take a look at the construction of a golden rectangle, Herz-Fischler, R. (1998) describes to construct a golden rectangle you start off with a square with sides ACDE and then construct a rectangle with the sides AB and CB and has the same are as square ACDE. This can be better seen in the following image:
We see that this construction gives \(ACAC=AB*CB \longrightarrow AB/AC = AC/BC\) which is the definition of the golden ratio. Check out this applet to see what happens when you construct multiple golden rectangles and see how the famous spiral forms from them. Golden Rectangles
The pentagram was one of the most used symbols of the Pythagoreans. The geometry of the pentagram apparently has many ratios where the golden mean occur, which leads us to believe the Pythagoreans knew about his ratio. Take for instance any pentagram as seen in the picture below.
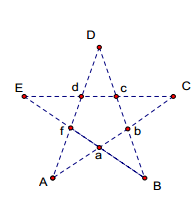
The diagonals bisect each other in a way that when you take the ratio of the two sides after being bisected they form a golden ratio.
A series of pentagons/pentagrams can be used to show the golden ratio in a different way. We see that they diagonals bisect each other in golden ratios as seen above. Another cool thing can be observed too. The larger of the two segments split by the diag0nal becomes the length of the side of the next smallest pentagon.
We end up with the recurrence \(s_{n}=d_{n-1}; d_{n}=d_{n-1}=s_{n-1}\) and if you choose \(s_{1}=2\)and \(d_{1}=3\) using these we get the sequence \(\dfrac{s_{n}}{d_{n}}=3/5,5/3,8/5,13/8, . . \) which is ratio of successive terms in the Fibonacci sequence which we know converges to what??? . . . THE GOLDEN RATIO!!!! To get a little closer look at these ratio's and discover some things out for yourself check out this app. Pentagram Applet
To see some of the mathematics here and the golden ratio explained in some other ways check out Khan Academies video on the golden ratio. Khan Academy