NATURE



Many of beauties of nature have the Fibonacci numbers and ratios evidenced in them.
The spiral is the most commonly associated with the Fibonacci sequence.





The nautilus shell expresses the Fibonacci sequence. This organism remained relatively unchanged for millions of years because of it's sound structure and is known as the "living fossil."





Many different flowers have a Fibonacci number for petal count.


Buttercups have 5 petals


Delphiniums have 8 petals.
Marigolds have 13 petals.
Asters have 21 petals.



And daisies have 34. Which is why you should always start with "He loves me not."

PHYLLOTAXIS

Phyllotaxis is how leaves arrange on a plant stem.
This can occur in two different types- whorled or spiraled. Whorled is where the leaves grow simultaneously.
The spiral pattern is created by use of the golden angle.




The apex of a plant, or plant tip, organizes the architecture of a plant.
With a logically approach it is understandable that in order to obtain maximum efficiency the leaves would want an arrangement so that all leaves absorb maximum sunlight,
this will occur when the leaves are arranged with the golden ratio.

The beginning stages of a leaf or flower, called a primordia, develop from the apex.
The angle between two consecutive primorida is called the divergance angle and is approximated to be 137 degrees- the golden angle.
As more and more primorida emerge the spiral will form. The primorida will be further away from the apex.



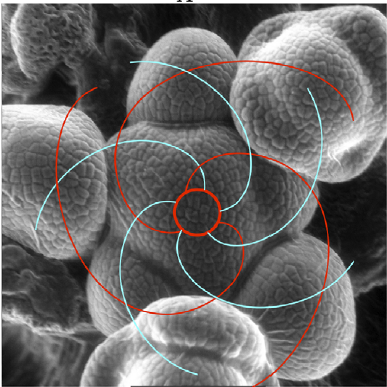
Two sets of spirals will be formed- one clockwise, one counterclockwise.
Parastichies are the imaginary spirals connecting the primorida.
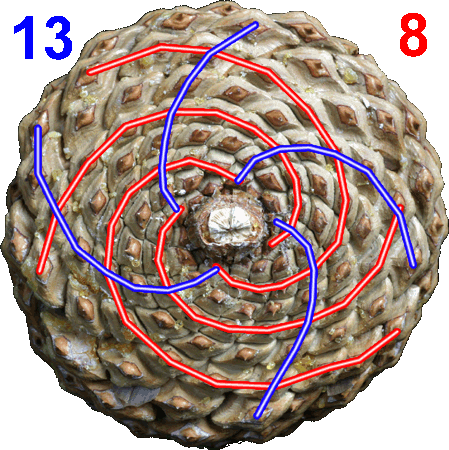
The number of spirals in each set will be two consecutive Fibonacci numbers.
As shown below, the clockwise set has 13 spirals and the counterclock wise set has 8.



Here is an applet I made to help better understand the how the golden angle maximized spacial arrangement.

DIVERGENCE ANGLE APPLET

Not every flower's seed arrangement will show a perfect 137.5 degree divergance angle. If the angle is slightly below or above 137.5, it will create gaps in the arrangment.
Although varying divergance angles create pretty patterns, only 137.5 will maximize efficiency in seed arrangement. The sunflower is a fantastic example of this. It's seeds are solid and bulky and have to be arranged with precision in order to keep them in the head of the sunflower. So sunflowers have a divergance angle of 137.5 degrees.