Millennia ago, artists were faced with a problem: How do they represent a three dimensional world on a flat, two dimensional canvas? Many artists avoided this issue by creating paintings without perspective, such as the following:

Notice how all the buildings and people in the painting are stacked on top of one another, in an unrealistic manner.
Giotto di Bondone
Artist Giotto di Bondone, an Italian painter and architect in the fourteenth century, is one of the painters credited with initiating perspective in art. Giotto started painting scenes in which he was able to create the impression of depth by applying mathematical rules to his artwork. Here is an example of his work:

Giotto used the technique of declining lines above eye-level as they moved away from the observer, and lines below eye-level were inclined upwards as they moved away from the observer, creating depth in space. This was the start of linear perspective in art.
So what is the math behind linear perspective in art?
Fillippo Brunelleschi
Artist Fillippo Brunelleschi is credited with the first correct formation of linear perspective. He understood that there should be a single vanishing point to which all parallel lines in a plane, other than the plane of the canvas, converge. Also important was his understanding of scale, and he correctly computed the relation between the actual length of an object and its length in the picture depending on its distance behind the plane of the canvas. Here is a visual example:
Brunelleschi used these mathematical principles in a new way. Brunelleschi drew two pictures of Florence on wooden panels with correct perspective. One was of the octagonal baptistery of St John, the other of the Palazzo de Signori. To give a more realistic demonstration of the accuracy of his painting, he bored a small hole in the back of the panel with the baptistery painting at the vanishing point. A spectator was asked to look through the hole from behind the panel at a mirror which reflected the panel. In this way Brunelleschi controlled precisely the position of the spectator so that the geometry was guaranteed to be correct.
Leon Battista Alberti
Leon Battista Alberti, an architect, writer and painter, was the first to write down rules of linear perspective in his treatise On Painting. Alberti was a strong advocate for the knowledge and application of mathematics and geometry for artists. Alberti said,
him above all to have a good knowledge of geometry."
-- Alberti (K. Andersen, p. 18)
Alberti described linear perspective as:
Alberti states:
"Here is a rule: As the angle within the eye becomes more acute, so the quantity seen appears smaller. . . Here I usually give my friends a similar rule: as more rays are used in seeing, so the thing seen appears greater; and the fewer the rays, the smaller" (On Painting, p.47).
An applet I created using GeoGebra reinforces this concept. I did not originally create this applet for this site, but upon reviewing it, I found that the principles shown in the applet coincide with those of Alberti.
While exploring this applet, notice how the size of the angle changes depending on the distance between you and the "barn door". This is the same principle that Alberti was expounding upon. The closer you are to an object, the larger the angle between you and that object will be, which corresponds to the size you should create that object in your artwork.
Albert did the following work on perspective geometry:
"A point, P, is determined on a panel. The distance from the base of the panel to this point is taken as proportional to the height of a man. The height of the man to be painted is divided into thirds to form the module for the divisions of the base line, A, B, C, etc. Lines are drawn from the point P through these divisions establishing the orthogonals PA, PB, PC. In another area (diagram 2) a straight line A', B', C' is drawn with the same divisions as marked on the base line of the quadrangle. Another line, HT, is drawn parallel to it and above it a distance O, equal to the distance from the centric point to the base line. On this line, the hight line, the proportionate distance from the eye of the observer to the panel is established, Di. Lines are drawn from this point to the divisions A', B', C'. These height-distance lines are cut by a line perpendicular to the height line. The intersection of these lines with the perpendicular establishes a set of values, A", B", C" which are transferred to the panel containing the orthogonals (diagram 3) to establish the recession of the transversals. These are checked with a diagonal, GZ, which determines the accuracy of the drawn."
(Leon Battista Alberti On Painting, John R. Spencer, p. 111-12)
The following diagram illustrates Alberti's theory:
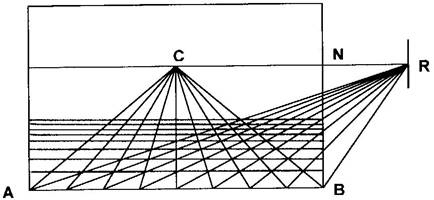
--Leon Battista Alberti
Alberti also gave direction on using this method to correctly project a circle onto a surface and obtaining the proper elliptical shape. Alberti introduced this subjected without knowing the importance that projecting conic sections would later have.
Here is an example of a painting that uses linear perspective. Note the differences between this painting and the ones above.
