The Developers of Vectors

To understand the history of vectors, it must be understood what the definition of a vector is. A vector is a line segment that has magnitude and direction. Hence, I will focus on the history behind three main mathematicians’ attempts to analytically graph direction and magnitude. All three attempts eventually led to the concept of vectors that we know of today as vector analysis. These three mathematicians are Caspar Wessel, William Rowan Hamilton, and Josiah Willard Gibbs.

It was interesting to me while researching out the history concerning the development of vectors how closely tied their development was to the development of the understanding of complex numbers. In fact, from my research into the origins of vectors, it became evident to me that the discovery of a complex number as a single point in the complex plain was the basis for the beginning of what we call today vector analysis. Casper Wessel was fundamental in the discovering that a complex number was a single point.

Caspar Wessel

Retrieved from http://www.norge.ru/wessel_caspar/

Much of my information concerning Caspar Wessel came from a book entitled, The History of Mathematics an Introduction 6th Edition by David M. Burton Pages 628-637. Burton said that Casper Wessel’s fame stems from one paper that he wrote in which he stated that his objective in writing the paper was to show how to represent direction analytically using line segments (basically vectors). He demonstrated two things in this paper. First, he demonstrated how to add them. The process that he used was the same process that we use today for adding vectors. Take for example two arbitrary line segments—segment a and segment b. In order to add segment b to segment a, place segment b at the tip of segment a and draw a line from the beginning of segment a to the end of segment b. The new segment that you create is the sum of segment a and segment b. (Burton, 2007, Pg. 629-630)

The second thing that Burton said that Wessel demonstrated was how to multiply two line segments. He did this by developing a coordinate system with axis +1 corresponding to 0 degrees, +e corresponding to 90 degres, -1 corresponding to 180 degrees and -e corresponding to 270 degrees. The following is an example of this coordinate system:



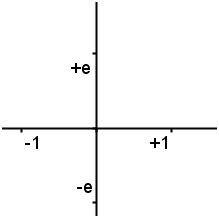
Then, using a rule that states that the direction angle of the product shall equal the sum of the angles of the factors, he multiplied all possible combinations of +1, +e, -1, -e to get the following:

(+1)*(+1)= +1

(+1)*(-1)= -1

(-1)*(-1)= +1

(+1)*(+e)= +e

(+1)*(-e)= -e

(-1)*(+e)= -e

(-1)*(-e)= +e

(-e)*(+e)= +1

(-e)*(-e)= -1

(+e)*(+e)= -1

From performing these calculations, Wessel found that e = the square root of -1. So, Wessel found that his coordinate plane is actually equivalent to what we call the Complex Plane for Imaginary Numbers. Burton goes on to say that, “He (Wessel) stated that any line segment can be represented by the expression a+b*e and derived the rule (a+b*e)*(c+d*e)=(ac-bd)+(ad+bc)*e”.(Burton, 2007, Pg. 630) Thus, Wessel had found a type of vector in the complex plane and a way to do vector addition and multiplication. The following is an general illustration of a line segment in the complex plane.



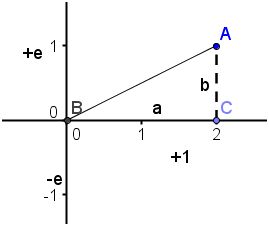
Burtain continued to say that that unfortunately Wessel's discoveries "lay burried for a century"(Burton, 2007, Pg. 630).

If you would like to learn more about Caspar Wessel, view the following website:

http://www-history.mcs.st-andrews.ac.uk/Biographies/Wessel.html



William Rowan Hamilton

(2010)

Burton said that William Rowan Hamilton tried to extend the idea of a+bi (I replaced e with the more common notation i) to triplets of the form a+bi+cj where i and j are both imaginary numbers and i^2=j^2=-1. However, Hamilton was only able to extend the idea of addition to triplets. He was unable to figure out a way to do multiplication with them.

Then one day in 1843, he was on a stroll with his wife. As they came to the Royal Canal in Dublin, Ireland, the solution to his problem came to his mind as if by revelation. It was to simply develop an expression with four terms of the form a+bi+cj+dk where i, j, and k were imaginary numbers and i^2=j^2=k^2=-1. Hamilton quickly pulled out a pocket notebook that he carried with him at all times and wrote down what he had discovered. His discovery became known as a Quaternion of the form q=a+bi+cj+dk. This was a vector in the Complex Number Plane of four dimensions.(Burton, 2007, pg. 634-637) The following is a picture of the Royal Canal in Dublin as well as a picture of a memorial to commemorate Hamilton's discovery:


(Torrissen, 2012)


(Dolan , 2010)

If you would like to learn more about Hamilton, view the following website:

http://www-history.mcs.st-and.ac.uk/Biographies/Hamilton.html



Josiah Willard Gibbs



(Josiah Willard Gibbs)

Lange, in his artical Josiah Willard Gibbs, said that Gibbs is known as the founder of our modern vector system. In the development of this system, Gibbs merged Hamilton’s idea of a quaternion with Herman Grassmann’s idea of an extension theory for limitless dimensionality(Langer, 1939, pg. 82-83). The online enclyopedia entitled, New World Encyclopedia said that to do so, Gibbs simply dropped the constant from the quaternion and maintained the vector part with the i, j, and k. Today, we still use the i, j, and k to differentiate between the components of a three dimensional vector, but they have no reference to imaginary numbers as they did for a quaternion(Josiah willard gibbs). Burton also said that Gibbs was the one who introduced two new methods of multiplication namely the dot product and the cross product (Burton, 2007, pg. 637).

Bork said that during the 1890s, there was a debate that took place between Gibbs and another mathematician by the name of Tait concerning using vectors in the form of a quaternion as opposed to the present day vectors as proposed by Gibbs. Gibbs argued that scalar addition and scalar multiplication could be extended to n-dimensions while it wasn’t necessarily proven that a quaternion could be extended to n-dimensions. Hamilton only proved it for the form q=a+bi+cj+dk. Also, remember that Hamilton couldn’t prove it for a triplet. Tait replies by asking Gibbs why students of physics need to use more than three dimensions.

Others, like mathematician Cayley, found the idea of a quaternion to be artificial. He compared a quaternion to a pocketbook that had to be unfolded and translated back into coordinates in order to be understood. His viewpoint makes sense if we remember that the quaternion is based off the Complex Number Plain. It’s hard to make sense out of a system based of imaginary numbers and apply it to the physical world (Bork, 1964, pg.331-333).

Despite the debates that took place, eventually, the vector system Gibbs created won out. It was superior in the fact that it had more flexibility and dynamics. However, the mathematical thought of Hamilton and Grassmann played a central role in the evolution of vectors. Therefore, scientists and mathematicians have reason to be grateful to all those who contributed to the development of vectors, not just Gibbs.

If you would like to learn more about Gibbs, view the following website:

http://www.aip.org/history/gap/Gibbs/Gibbs.html