Applications of Vectors

The following are a few examples of the many applications of the basic properties of vectors that were explained on the page "The Basics of Vectors". Below, there are a few video clips and two Geogebra applets that will allow you to investigate the application of vectors.

Applications of Vector Addition/Subtraction

The following Youtube clip by AlRichards314 explains how vector addition can be used to find displacement and the direction of that discplacement. It gives three different examples of applications of vector addition. Click on the following link to view it:

Three Application of Vector Addition (AlRichards314, 2011)

Application of the Dot Product

The following Youtube clip by AlRichards 314 explains how the dot product can be used to find the angle between two vectors. It also explains how it can be used to find the projection of one vector onto another vector. Click on the following link to view it:

Angle Between Two Vectors and Projections (AlRichards 314, 2011)

Application of the Cross Product

The following Youtbue clip by bullcleo1 illustrates how vectors are very useful for modeling force, especially a special kind of force called torque. It provides an example of how the cross product can be applied to solve for torque using both the component form of the cross product and the non component form of the cross product.

Special Application of Cross Product using Torque (bullcleo1, 2010)

Application of Vectors to Map a Path in a Plane or a Particle in Space

Stewart, in his book Calculus: Contexts and Concepts, explains how the concept of vectors can be extended to contain components of polynomial form. They can be written as, r(t)=(f(t),g(t)) or r(t)=(f(t),g(t),h(t)) or with many more components depending on the dimensionality of the coordinate system. These type of vectors are most often useful for describing the path of a particle in space for a three-dimensional plane or mapping out a path in a plane (Stewart, 2005, pg. 695-700). The following Geogebra applet allows students to adjust the coordinates of a vector with a x component in the function form of f(x) and a y component in the function form of g(x).

Vector Paths

The above applet focused on vector paths in two-dimensional planes. The following is a picture of a curve created by a vector mapping out the path of a particle in a three-dimensional coordinate system.


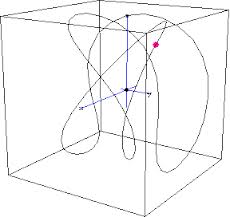
(n.d.). Retrieved from http://people.usd.edu/~jflores/MultiCalc02/WebBook/Chapter_14/Graphics/Chapter14_1/Html14_1/14.1 Vector Functions and Space Curves.htm

Application of Vectors to Matrix Algebra

George Nakos and David Joyner teach how vectors are a very big part of Matrix Algebra in their book Linear Algebra with Applications. The following are just a few ways:

• A mX1 matrix is a vector (Nakos, 1998, pg. 154).

• Matrix multiplication of matrix A with matrix B involves multiplying each row matrix of A with each column vector of B. Basically what is being performed is the dot product to produce the new elements in the resulting matrix AB(Nakos, 1998, pg. 158-159).

• Using matrices to solve systems of equations. Take for example the following equations:

2x+y=10
3x+6y=42

They can be written in the form AX=b where A is the matrix containing the coefficients of the equations and X is the vector containing the variables x and y and b is the vector containing the solutions 10 and 42. In other words:



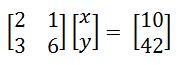
Then if A is invertible, you can solve for the variables in X by X=bA^(-1) (Nakos, 1998, pg. 169-171).

The following applet demonstrates matrix multiplication. It also demonstrates how adding and multiplying two matrices is similar to adding two vectors and doing the dot product on two vectors. Even though a row in a matrix is not exactly a vector, I treated the row matrices as vectors, just like the column vectors to demonstrate how similar the operations between matrices and vectors are.

Vectors and Matrices