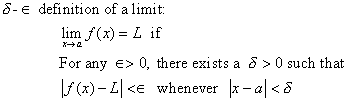Delta Epsilon

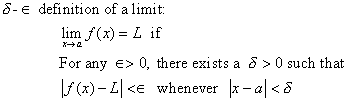
• The phrase "for every ∈ >0 " implies that we have no control over epsilon, and that our proof must work for every epsilon.

• The phrase "there exists a δ>0 " implies that our proof will have to give the value of delta, so that the existence of that number is confirmed. Typically, the value of delta will depend on the value of epsilon.

• The phrase "such that for every x" implies that we cannot restrict the values of x any further than the next restriction provides.

• The phrase "the expression 0<|x-a|<δ" is the starting point for a series of implications (algebra steps) which will conclude with the final statement.

• The expression " |x-a|<δ " means that the values of x will be close to a, specifically not more than (nor even equal to) delta units away. The expression 0<|x-a| implies that x is not equal to a itself.

• The phrase "implies |f(x)-L|< ∈ " is the conclusion of the series of implications. Once this statement is reached, the proof will be complete.

Referenced from this site

Using the Delta Epsilon Proof

What does it really mean?
We know from the informal definition that f(x) gets closer to some limit as x gets close to some value.
To simplify this, lets say that f(x) gets close to “L” as x gets close to “a”.

What does it mean to “get close”?
|x-a| is a good way of demonstrating how close x is to a
|f(x) – L| is a good way of showing how close f(x) is to L.

So when |x-a| is small, so is |f(x)-L|.
Let δ and ∈ be small values, such that ∈>0, δ>0, and x is not equal to a, or 0 < |x-a|.
Then |f(x)-L| < δ and |x-a| < ∈.
Then 0 < |x-a| < ∈ and 0 < |f(x)-L| < δ
However, we want the first part to imply the second part.

For example we want to prove that lim( x-> 3) 2x+4 =10
Using the formal definition we see that:
0< |(2x+4) -10| <δ and 0 < |x-3| < ∈
|(2x+4) -10| <δ
|2x-6|<δ
2|x-3| < δ
|x-3|<δ/2

We know |x-3|< ∈ so we can guess delta=δ/2

0<|x-3| < ∈
0<|x-3|< δ/2
0<2|x-3|<δ
0<|2x-6|<δ
0< |(2x+4) -10| <δ

For more details visit this site

Check out these geogebra applets from the web to learn more!
Delta Epsilon Limits

Epsilon Delta Definition