Definition of a Limit

The topic of limits tends to be a person’s first experience with “Philosophical Mathematics”. Instead of just crunching numbers, you start considering more complex questions such as, “Even though this function is undefined at this x-value, what height did it intend to reach?”¹

Limits can also be a person’s first experience in really hating mathematics. It might be because the definition of a limit looks like this:



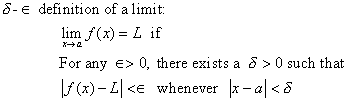
Let f be a function defined on an open interval containing a (except possibly at a) and let L be a real number. Then for all real ∈ > 0 there exists a real δ > 0 such that for all x with 0< |x-c| < δ, we have |f(X)-L| < ∈ ²

Intimidating.

Informally, “A limit is the intended height of a function at a given value of x, whether or not the function actually reaches that height at the given x.” ¹