The Complex Plane

Rectangular Coordinates The Complex Plane is a tool we can use to express complex numbers as a point or position vector in a 2-d Cartesian coordinate system. The horizontal axis represents the real part of the complex number. The vertical axis represents the imaginary part of the complex number. The point z = x + yi can be identified with rectangular coordinates (x,y), where x is the real value and y is the imaginary value. So, just like with regular ordered pairs, we graph the point z by going horizontally x units and vertically y units.

Polar Coordinates The point z = x + yi can also be expressed with polar coordinates (r,θ). x = rcosθ and y = rsinθ z = |z|(cosθ + isinθ) r is the distance from the origin to z which is known as the modulus; r = (x2 + y2) = |z| θ is the angle between the positive real axis and the line segment from 0 to z and is called the argument of z, denoted by θ = argz.

So how do we convert between rectangular and polar coordinates??

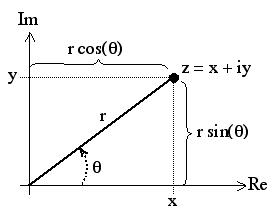
Rectangular to Polar Coordinates Given z = a + bi, to convert to polar coordinates, one must simply use the following: r = (a2 + b2)(1/2). Notice it's like doing the pythagorean theorem! θ = arctan (b/a).

Polar to Rectangular Coordinates Given (r,θ) we can convert z into rectangular coordinates (a,b) by plugging the values of r and θ into a = rcosθ and b = r sinθ

Find the modulus and argument of:
6
8i
-4+4i
2-7i.
You can practice on your own and check your answers here:
Original applet - Converting Polar and Rectangular Coordinates
Need extra help? Check this out: Complex Numbers