History of Geometry

Euclid is believed to have been born and have lived around the time of 300 BC. It is intriguing that
no personal journal or records kept that tell about Euclid's life outside of Mathematics have been found. He studied
in Alexendria at the best of schools there and best known to the world for his treatise written on geometry.
The Elements , as it is titled, contains thirteen books that range from topics anywhere from simple definitions
of a point and a line, to theorems proving the square root of two as a irrational number. Though this book was written over
2000 years ago, it has stood the test of time and become one the most imporant texts in mathematics. In addition to the
actual theorems and mathematical content that Euclid left behind, just as imporant was the structure by which
he constructed his seemingly new branch of mathematics.
For centuries, this was believed to be the
greatest discovery of mathematics. Rene Decartes was a French philosopher, mathematician, and writer most notably known
now for the Cartesian Coordinate System, which was named after him. He was a very well educated man, but of all that
he studied he wrote of mathematics that "Of all those who have hitherto sought for truth in the Sciences, it has
been the mathematicians alone who have been able to suceed in making any demonstrations,
that is to say, producing reasons which are evident and certain" (Kline, 43). Euclids foundation of definitions,
axioms, and
proven postulates and theorems were the bigging of proven mathematics, first by simple construction.
The Elements was originally written in Greek; however, throughout time it has been translated in to
many different languages. Because of this the wording through translation can vary. Below are few of the Definitions, Common Notions,
and Postulates recorded by Euclid.
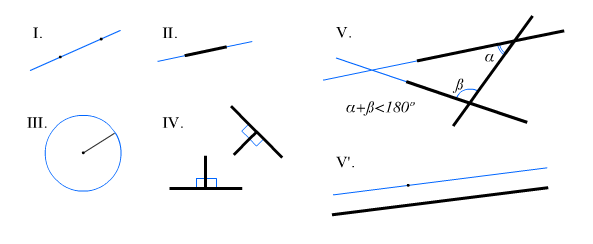
Definitions :
a. A point is that which has no parts.
b. A line is breadth less length.
c. A strait line is a line that lies evenly with the points on itself.
Common Notions & Axioms :
1. Given two points there is one straight line that joins them.
2. A straight line segment can be prolonged indefinitely.
3. A circle can be constructed when a point for its center and a distance for its radius are given.
4. All right angles are equal.
5. If a straight line falling on two straight lines makes the interior angles on the same side leess than two right angles, the two straight lines, if produced indefinitely, meet on that side on which the angles are less than the two right angles.
6. Things equal to the same thing are equal.
7. If equals are added to equals, the wholes are equal.
8. If equals are subtracted from equals, the remainders are equal.
9. Things that coincide with one another are equal.
10. The whole is greater than a part.
Postulates:
1st Postulate: A strait line segment can be drawn joining any two points.
2nd Postulate: Any straight line segment can be extended indefinitely in a straight line.
3rd Postulate: Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center.
4th Postulate: All right angles are congruent.
5th Postulate: If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, then the two straight lines if extended will meet on that side of the strait line on which the angles are less than two right angles.
Hundred of years after Euclid, when the Church, centered in Rome, took great hold on the politics and had a powerful influence in the educational
realm, many intellectual invdividuals no long sought for reason alone, but many followed in the footsteps of their predecessors
and were convinced that "God was a skilled mathemtician and physicist."
Newton stated in December of 1692:
"To make this [solar] system, therefore, with all its motions, required a cause which understood, and compared together the
quantities of matter in the several bodies of the sun and planets, and the gravitating powers resulting from thence; the several
distances of the primary planets from the sun, and of the secondary ones...from Saturn, Jupiter, and the Earth; and the velocities
with which these planets could revolve about those quantities of matter in the central bodies; and to compare and adjust all these
things together in so great a variety of bodies, argues that cause to be not blind or fortuitous, but very skilled in mechanics and geometry" (Kline, 59).
Carl Friedrich Gauss (1777-1855), a German mathemtician and physist, believed up until 1799 that Euclid’s geometry was acutally the geometry
of physical space.
However, compared to the previous four Postulates, Euclid's Fifth Postulate was much more complex and lengthy. Through the years since Euclid’s time, there were many mathematicians and scientists that had
been troubled by this discrepancy. Mathemticians
sought to make Geometry concrete once by fixing this last postulate.
There were a few different ways that were attempted by mathematicians to resolve the problem created by
Euclid’s 5th postulate. The first was to replace the parallel axiom by a more self-evident or understandable
statement. The second was to deduce the parallel axiom from the other nine of Euclid’s axioms. Why did Euclid not
state that if the sum of angles 1 and 2 was 180 degrees, then the lines would never meet? Perhaps he was unsure
if that was true.
In the late 18th Century, John Playfair(1748-1819) wrote his version of the Euclid's 5th Postulate.
"Through a given point P not on a line l there is one and only
one line in the plane of P and l which does not meet l.

This is the most commonly used definition in High Schools today. Generally called the Parallel Postulate,
it is a much more clear and concise wording.
It is by way of this Fifth Postulate that Planar, now known as Euclidean Geometry, was not the only geometry created. When
mathmeticians realized that other geometries could be created if this last postulate was re-written, they broke off and
began to create what were called "Non-Euclidean" Geometries. Non-Euclidean geometry is any geometry that is different from Euclidean geometry.
Each Non-Euclidean geometry is a consistent system of definitions, assumptions, and proofs that describe
such objects as points, lines and planes. The two most common non-Euclidean geometries are spherical
geometry and hyperbolic geometry. The essential difference between Euclidean geometry and these two
non-Euclidean geometries is the nature of parallel lines: In Euclidean geometry, given a point and a
line, there is exactly one line through the point that is in the same plane as the given line and never
intersects it. In spherical geometry there are no such lines. In hyperbolic geometry there are at least
two distinct lines that pass through the point and are parallel to (in the same plane as and do not
intersect) the given line. There three well defined and used geometries today, Hyperbollic,
Euclidean, and Elliptical/Spherical. As pictured below, one can see that each geometry has a unique
style of line or curves. Euclidian geometry (pictured on the bottom) has straight curves, while Hyperbolic geometry
(pictured in the center) has negative curvature, and Elliptical and Spherical geometry is defined
by positive cuves. Because of this, the very nature of a triangle is altered. For example, in Euclidean
geometry a triangle has a consistent degree measure of 180. Because of the positive curvature characteristic of
Elliptical geometry, triangles have degrees larger than 180 degrees.

Today, we can learn of three main type of geometries. Euclidean Geometry is the most common and is taught in High
Schools today. Why is that? Poincare, most known for his conjecture about three dementional space that was not solved until
the 21st Century, studied 3-Dimentional space and geometry. He, however, insisted that we would always use Euclidean geometry with the usual interpretations of straight line, that is,
the strethed string or the ruler's edge, because it is simpletst" (Klein, 343). Spherical Geometry and/or Elleptical Geometry are very similar in characteristics to one another, and though
they seem abstract to one is only familiar with two-dimensional geometry, we use it everytime we map something out
on a globe. Instead of a line that has only breadth because of its being a line in Euclidean Geometry, a line in Spherical
Geometry consists of a circle traced on the sphere where the plane of two points divides the hemisphere in to two equal parts. Refer to the
images below.

The angles of Spherical Geometry defined as angle between the two lines is then defined to be the angle between
the two planes formed by the great circles.

For further definitions click here. These are great simple definitions for Spherical Geometry.
The lines of Longitude and Latitude that create a grid system on the earth are based upon the great circles created
by the lines drawn on the Earth's sphere.

The history of Mathematics, and geometry in particular, teaches us that the body of mathematics is continously
growing. Who knows when the next big thing will come and change the way we view the mathematics that we already have?
Mathematics is used today in so many ways including computer graphics, mathematical modeling for architects, and medical
diagnosis. I hope that the students of today can see that they can be the future of growing mathematics tomorrow!






